A l’approche choc Paris-Barça, j’avais envie de vous parler de coup franc.
Avec leurs trajectoires de balles parfois incroyables, ces phases de jeu ne cessent de fasciner.
Mais saviez-vous qu’un coup franc ne se tire pas pareil en été et en hiver? Comprenez-vous pourquoi votre ballon de plage ne prend jamais l’effet attendu?
Ensemble, faisons un rapide tour d’horizon de ce que la science nous a appris du coup-franc.
Balle au centre – on parle de quoi?
Quiconque a déjà shooté dans un ballon sait que, pour courber la trajectoire du ballon, il est important de bien « brosser » sa frappe. Brosser sa frappe consiste simplement à frapper le ballon sur le côté afin de lui communiquer un mouvement de rotation sur lui même, un peu comme si on le faisait avec les poils d’une brosse en fait.
Nous allons voir comment ce simple mouvement de rotation va permettre d’infléchir la trajectoire du ballon pour mieux contourner le mur et tromper le gardien de but.
Explication du phénomène par la mécanique des fluides (application simple de l’équation de Bernoulli)
La démonstration la plus souvent utilisée pour décrire ce phénomène fait appel à la plus fondamentale des lois de la mécanique des fluides. Dans ce modèle, on invoque en outre régulièrement l’effet Magnus, du nom de son papa : un physicien allemand du XIXème siècle, né sans doute trop tôt pour avoir un jour shooté dans un ballon de football.
Pour comprendre ce phénomène vous devez admettre deux choses:
- plus l’air se déplace vite, plus sa pression est faible (pour les initiés, cela découle de l’équation de Bernoulli)
- un objet placé dans un gradient de pression aura toujours tendance à se déplacer vers les pressions les plus faibles.
Exemple simple :
Pour vous en convaincre, prenez une feuille en papier à son extrémité puis soufflez au dessus de la feuille.
L’air soufflé au dessus de la feuille aura une vitesse plus élevé que l’air situé sous la feuille. La pression sera donc plus faible au dessus de la feuille.
Vous observez alors que la feuille se redresse pour se déplacer vers les zones de pressions les plus faibles
En fait, c’est exactement le même effet qui explique la trajectoire courbée du ballon de football.
Application au ballon de football:
Lorsque vous shootez ‘normalement’ dans le ballon (ie sans brosser votre frappe), le ballon se retrouve propulsé dans les airs.
De l’air se déplace alors à grande vitesse le long de la surface du ballon.
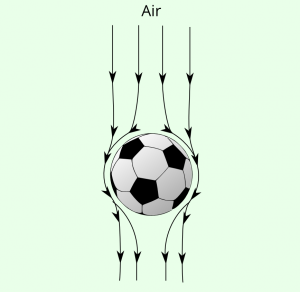
L’écoulement est symétrique par rapport à l’axe de la trajectoire de la balle, l’air s’écoule à la même vitesse sur toutes les faces du ballon, il n’y a donc pas de différentiel de pression.
Maintenant si vous recommencez votre frappe en la brossant (ie en confiant au ballon un mouvement de rotation sur lui même)
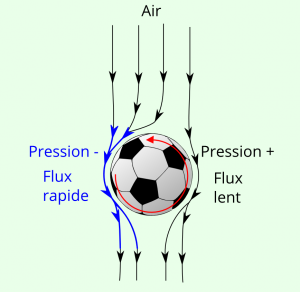
L’air va accélérer sur l’un des côtés du ballon (lorsqu’il va dans le même sens que la surface) et va freiner sur l’autre côté du ballon lorsqu’il est opposé au mouvement de rotation de la surface. Ceci s’explique par les frottements que rencontre l’air avec la surface de notre ballon.
Dans cette situation, la vitesse est plus élevée sur l’un des côtés du ballon. Dans notre exemple, la pression sera donc plus faible sur la face gauche du ballon et sa trajectoire aura donc tendance à se courber vers la gauche.
Application des principes au très contrariant ballon de plage (introduction à l’écoulement de fluide visqueux)
On aurait presque pu s’arrêter là… (et d’ailleurs les lecteurs impatients le feront) mais c’était sans compter sur le retour du soleil et le souvenir chaque jour plus présent de ce maudit ballon de plage. Ce ballon qui a toujours choisi de prendre la courbure inverse quand je tentais vainement de l’enrober vers une lucarne imaginaire.
Alors pourquoi nos plus beaux effets ne marchent-ils pas à la plage?
Tout d’abord, non ce n’est pas qu’une question de vent, essayez en intérieur, le constat est le même.
Pour comprendre l’inversion du phénomène, il va falloir d’abord se résoudre à aller un peu plus loin dans la description de l’écoulement de l’air autour du ballon, l’équation de Bernoulli (relation vitesse-pression) ne suffisant manifestant plus à décrire ce que nous observons.
En fait nous allons montrer que l’effet Magnus fait intervenir un deuxième phénomène capable de dévier le ballon : la déviation de la force de traînée. Nous allons même voir que dans certaines conditions (avec un ballon de surface lisse notamment), ce deuxième phénomène peut conduire à l’inversion du signe de la force de Magnus (et renverser la courbure de la trajectoire du ballon, rien que ça…).
Mais avant de comprendre comment ce phénomène intervient, commençons par voir comment se passe l’écoulement d’un fluide visqueux autour d’un ballon qui n’est pas en rotation.
Écoulement d’un fluide visqueux et introduction à la force de traînée:
Tout d’abord, lorsque les premiers scientifiques ont essayé de décrire l’écoulement d’un fluide visqueux dans un conduit ou autour d’un objet, ils se sont rendus compte que ce dernier évoluait significativement en fonction de trois variables : (i) la vitesse du fluide v, (ii) la masse volumique du fluide  et (iii) la viscosité dynamique du fluide
et (iii) la viscosité dynamique du fluide  .
.
De facto, pour décrire les différents écoulements possibles, Osborne Reynolds (un ingénieur irlandais) a choisi de créer un nombre sans dimension regroupant ces trois facteurs (Re= vL/
vL/ ) et a commencé à étudier la structure des écoulements en fonction de ce nombre.
) et a commencé à étudier la structure des écoulements en fonction de ce nombre.
La seule chose que vous avez besoin de comprendre à ce niveau, c’est que le nombre de Reynolds Re fait intervenir:
 et
et  qui seront constants sur notre match de football (ils ne dépendent que de la météo).
qui seront constants sur notre match de football (ils ne dépendent que de la météo).- L: une longueur caractéristique qu’on considérera constante pour un type de ballon donné.
- et v : la vitesse de l’air (et donc du ballon) qui dépendra de la force de frappe du tireur.
Une fois ceci dit, il faut comprendre que lorsqu’un fluide visqueux s’écoule autour d’un objet, un petit coussin de fluide se forme à la surface de l’objet. Dans ce coussin, la vitesse du fluide est quasi nulle (comme s’il était collé au ballon). Ce coussin est communément appelé « couche limite ».
A l’endroit où la couche limite se décolle, à l’arrière du ballon, elle laisse place à un sillage turbulent où les vitesses des particules fluides sont augmentées, ce qui entraîne une chute de la pression (c’est la traînée blanche que vous observez derrière les avions).
Or, rappelez vous l’expérience de la feuille, différence de pression implique force tendant à déplacer l’objet. En fait cette force est appelée force de traînée et tend à freiner notre ballon.
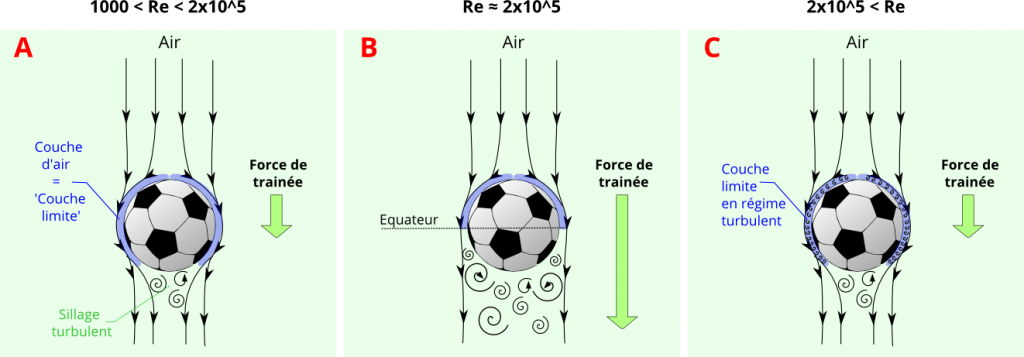
En fonction de la vitesse du ballon et donc de Re, nous observons deux différentes phases:
- Jusqu’à Re= 2×10^5 [de A à B], plus vous frappez fort dans le ballon, plus vous augmentez sa vitesse. Or plus vous augmentez la vitesse du ballon, plus la couche limite sera courte et le sillage turbulent large et donc plus la force de traînée sera importante. En gros, plus vous tirez fort, plus le ballon est ralenti par frottement, jusque là pas de scoop…
- Lorsque Re dépasse 2×10^5 [C] , il se produit un phénomène étonnant qui s’appelle la crise de traînée. En gros, les particules d’air de la couche limite jusqu’alors quasi immobiles se mettent à bouger de façon chaotique et consomment donc en partie l’énergie que se gardait bien égoïstement le sillage turbulent. Conséquence, lorsque Re dépasse 2×10^5, le sillage turbulent rétrécit et la force de traînée diminue soudainement.
En fait, sans le savoir, vous avez tous déjà observé ce phénomène de crise de traînée en shootant dans un ballon de plage.
En effet, quand vous shootez dans un ballon de plage, ce dernier part très vite (Re est supérieur à 2 x10^5), puis au bout de quelques mètres le ballon s’arrête brutalement (son Re vient de passer sous la barre des 2×10^5).
Alors pourquoi je n’observe pas ce phénomène de crise de traînée avec mon ballon de football?
Et bien en fait si, au football ce phénomène existe bien et peut notamment s’apercevoir sur les dégagements de gardien. Toutefois, le freinage du ballon de football est beaucoup moins marqué qu’avec un ballon de plage pour deux raisons:
- L’inertie d’un ballon de football est plus importante que celle d’un ballon de plage,
- La rugosité d’un ballon de football (de part ses coutures notamment) est plus importante, ce qui a pour effet de baisser significativement la vitesse limite à laquelle se produit la crise de traînée. Par conséquent, le freinage (transition Phase C → Phase B (figure4)) se produit à des vitesses plus faibles. [En fait pour un ballon de football, le nombre de Reynolds limite n’est pas de 2×10^5 (vrai pour un ballon lisse) mais de 10^5]
C’est notamment pour maintenir une rugosité importante que les fabricants continuent de garder les coutures sur leur ballon alors qu’ils sauraient très bien s’en affranchir par moulage. A ce tire, le Jabulani d’Adidas est réalisé par moulage, mais sans surprise les coutures ont été remplacées par des rainures destinées à maintenir une certaine rugosité de surface.
Et notre effet inverse dans tout ça?
Et bien, il découle directement de tout ce qui a été dit plus haut. Sauf que lorsque vous ajoutez au ballon une vitesse de rotation sur lui même, votre couche limite (collée au ballon) n’a plus une vitesse nulle mais tourne avec le ballon. La vitesse du fluide à prendre en compte pour le calcul du nombre de Reynolds est donc la vitesse relative de l’air par rapport à la couche limite. Et cette vitesse relative change donc selon que l’air s’écoule dans le sens de rotation du ballon ou en sens inverse.
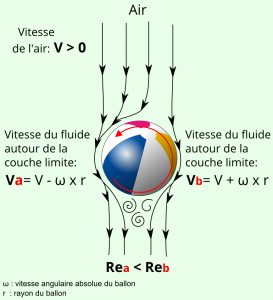
Et cette asymétrie des nombres de Reynolds va provoquer un effet magique.
Lorsque vous shootez dans votre ballon et que sa vitesse diminue, le ballon passe par une phase où l’une de ses faces possède un nombre de Reynolds > 2×10^5 et l’autre face un nombre de Reynolds < 2×10^5.
Cette crise de traînée asymétrique provoque alors un décalage du sillage turbulent (une couche limite est plus courte que l’autre) et va alors modifier l’orientation de la force de traînée.
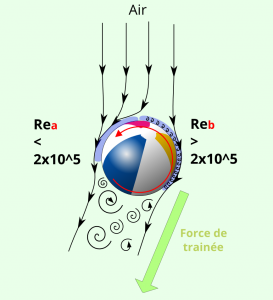
Notre force de traînée n’étant plus dans l’axe de la trajectoire de la balle transmet un moment à notre ballon déviant sa trajectoire vers la droite.
Conclusion – Influence de déviation de la force de traînée sur un terrain de football
Si vous avez bien suivi ce qui été dit plus haut, vous avez compris que l’effet Magnus, permettant de modifier la courbure de vos trajectoires de balles, est le fruit de deux phénomènes physiques pouvant, dans de rares cas, s’opposer l’un à l’autre.
Vous pourriez alors être tentés de vous demander s’il n’est pas possible d’inverser la force de Magnus avec un ballon de football (comme pour le ballon de plage).
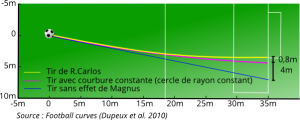
Et bien, en partie oui… en tout cas il est mathématiquement possible d’opposer temporairement les deux phénomènes. Personnellement, je pense ne l’avoir vu qu’une seule fois à l’oeuvre [en 1997 au stade de Gerland avec Monsieur Roberto Carlos à la réalisation [souvenirs ici]].
Toutefois, en pratique, la rugosité du ballon de foot ne permet pas une véritable inversion de la force de Magnus.
En effet, comme expliqué plus haut, la rugosité de la surface d’un ballon de football diminue le nombre de Reynolds limite nécessaire à l’apparition de la crise de traînée (10^5 pour un ballon de football contre 2×10^5 pour un ballon de plage). Par conséquent, les ballons de football possèdent presque constamment leurs deux couches limites turbulentes [Phase C décrite en figure 4] (ce qui rend les trajectoires plus stables). Ainsi, pour faire passer la couche limite de l’une des faces du ballon de football en régime laminaire [Phase A et B décrites en figure 4] il faut que la vitesse de la couche limite (ωxr) soit suffisamment proche de la vitesse linéaire de la balle pour que :
V-ω x r < 10^5 x  /
/  L
L
Le problème étant que même si les couches limites turbulentes se décollent plus difficilement que les couches limites laminaires, si l’on augmente fortement la vitesse de rotation du ballon, la couche limite turbulente (à droite dans la figure 6) se décollera tout de même un peu plus en amont et la force de traînée s’en trouvera moins déviée que sur le schéma.
Ainsi, la déviation de la force de traînée peut permettre d’atténuer l’effet de la force Magnus sur une partie de la trajectoire du ballon (par asymétrie de la crise de traînée). Une fois la couche laminaire repassée en régime turbulent, l’effet Magnus ‘traditionnel’ reprendra le dessus et la courbure de la trajectoire s’amplifiera à la dernière minute.
Enfin, pour ceux qui aimeraient postuler au poste de latéral gauche du Brésil, sachez que pour reproduire un tel exploit, la météo n’est pas à négliger.
En effet, en prenant r=L=11cm; et une frappe à 130 km/h (vitesse enregistrée lors du France-Brésil de 1997);
sachez que la vitesse de rotation à transmettre au ballon pour atténuer l’effet Magnus varie de presque 10% entre l’hiver et l’été.
A vos thermomètres donc!
Références:
Deux versions du très bon papier de ces messieurs David Quéré et Christophe Clanet.
http://www.editions.polytechnique.fr/files/pdf/EXT_1615_9.pdf
http://iopscience.iop.org/1367-2630/12/9/093004/pdf/1367-2630_12_9_093004.pdf
Quelques cours et articles traitant du sujet:
http://ethesis.inp-toulouse.fr/archive/00000567/01/elakoury1.pdf
http://e2phy.in2p3.fr/2008/documents/presentations/Cours_Etienne_Guyon.pdf
http://webinet.blogspot.fr/2010/06/le-jabulani-se-prend-il-pour-une-banane.html



Je trouve votre article très intéressant, perso j’adore le foot