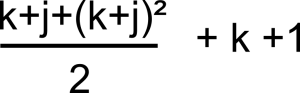« Nul ne doit nous exclure du Paradis que Cantor a créé».
Alors, c’est sûr que jeté comme ça, ça claque un peu moins qu’un tube de Polnareff. Mais ce message de soutien adressé par Hilbert au très décrié Georg Cantor sent bon la topologie et la lemniscate [1], et ça on aime (sisi vous allez voir)! Aujourd’hui, nous allons comprendre ensemble pourquoi Cantor n’avait pas beaucoup de copains en 1875 et en quoi l’homme a révolutionné notre perception du monde et de l’infini.
Introduction sommaire à ce qui n’est pas fini
Il existe deux façon de définir une notion. La première est de décrire ce qu’elle est, la seconde, bien sûr, est de décrire ce qu’elle n’est pas, et c’est de cette manière qu’est introduit le concept d’infini (à l’instar d’autres notions comme « indéfini » ou « incompréhensible »). Pourtant ce mot hétérologique [2] ,souvent retrouvé en philosophie, métaphysique ou théologie, n’a pas toujours trouvé son pendant mathématique. Descartes niait d’ailleurs l’existence d’un infini mathématique, lui reprochant notamment de décrire une vérité inaccessible à nos pauvres esprits finis.
Et, logiquement, lorsque Cantor créa sa théorie autour de l’infini mathématique, il s’attaqua vite aux conclusions cartésiennes, leurs préférant l’analyse de Spinoza pour qui il est absurde de concevoir l’entendement humain comme quelque chose de fini.
Finalement, quand Georg Cantor débarque en 1875 avec une théorie des ensembles toute neuve intégrant l’infini comme une entité mathématique propre, on ne l’accueille pas avec des cotillons et des langues de belle–mère.
Et pourtant… la théorie des ensembles de Cantor va marquer définitivement notre entrée dans l’ère des mathématiques modernes et avec elle va venir la conviction que tous les infinis ne se valent pas, certains étant manifestement plus grands que d’autres.
Quand quelques années plus tard, David Hilbert tentera d’illustrer en conférence la théorie de Cantor, on raconte qu’il utilisa l’exemple que je m’apprête à vous présenter.
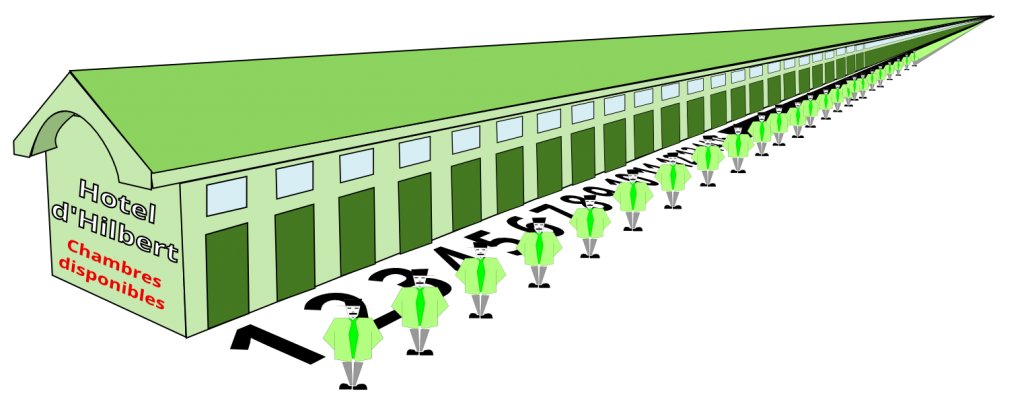
Bienvenue dans l’hôtel de Hilbert.
Unique en son genre, notre hôtel propose une infinité de chambres, toutes identiques et numérotées de 1 jusqu’à l’infini. [Chambre 1, Chambre 2, …, Chambre 2806, … etc…]
Arrivée de clients à l’hôtel – Additionner et multiplier l’infini
Le premier soir un nouveau client arrive à l’hôtel et semble déçu à la lecture de la note d’information affichée au dessus du comptoir.
Note d’information : Nous informons notre aimable clientèle que, victime de son succès, toutes les chambres de l’hôtel sont occupées pour la nuit.
Pourtant le gérant de l’hôtel se veut rassurant et propose vite une solution au nouvel arrivant. Il prend alors son microphone et s’adresse à l’ensemble de l’hôtel par le biais de hauts-parleurs.
Il demande alors à tous ses clients de bien vouloir changer de chambre pour se déplacer vers la chambre avec un numéro immédiatement supérieur à la leur, de sorte que le locataire de la chambre n aille dans la chambre n+1.
Ainsi, à la fin de l’opération la chambre 1 est disponible et peut accueillir notre nouveau client.
Plus tard dans la soirée, ce n’est plus un client qui arrive au comptoir mais un bus avec une infinité de clients numérotés C1, C2, C3,… jusqu’à l’infini.
Pourtant, une fois encore, le gérant reste calme. Avec le même flegme, il prend alors son microphone et demande à ses clients de changer une nouvelle fois de chambre. Chaque client devant se rendre dans la chambre ayant un numéro deux fois supérieur à la sienne. De sorte que le client de la chambre n se trouve alors déplacé dans la chambre 2n.
L’ensemble des chambres impaires se retrouvent alors libérées pouvant alors accueillir les nouveaux arrivants de telle sorte que l’arrivant Cn aille dans la chambre 2n-1.
Encore plus fort…
Le lendemain, tous les clients ont quitté l’hôtel. Mais le soir venu, ce n’est pas un bus qui arrive mais une infinité de bus (numérotés B1, B2, B3,…) contenant chacun une infinité de passagers (numérotés Ck-1, Ck-2,Ck-3,… avec k le numéro du bus dans lequel le client se trouve assis)
Et devinez quoi? Une fois encore le gérant de l’hôtel, placide, semble avoir la solution pour héberger tout ce petit monde.
Il demande alors au client C1-1(premier client du premier bus) d’aller dans la chambre 1, puis aux clients C1-2 et C2-1 d’aller respectivement dans les chambres 2 et 3.
En fait, il demande à chaque client Ck-j de se diriger dans la chambre numéro :
A travers ces exemples, l’hôtel de Hilbert nous montre que deux ensembles tels que l’un est strictement inclus dans l’autre peuvent toutefois avoir un même nombre d’éléments (en mathématiques on dit qu’ils sont alors équipotents).
Et ça, ça a pas mal troublé les mathématiciens de l’époque car cette proposition est complétement fausse pour les ensembles finis… et oui, si votre hôtel (qui n’est pas un hôtel avec un nombre infini de chambres) a toutes ses chambres d’occupées… et bien c’est marre, il ne pourra pas vous accueillir (voir le principe des tiroirs de Dirichlet [3]).
Arrivée d’un bus un peu spécial – Tous les infinis ne se valent pas
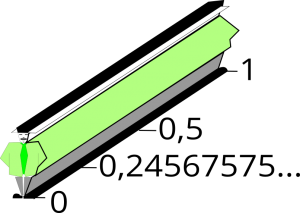
Enfin le dernier soir, c’est un bus un peu particulier qui se présente devant l’hôtel. Le bus contient bien une infinité de passagers mais ces derniers ne sont pas disposés comme les bus précédents. En effet, les sièges semblent infiniment resserrés et au lieu d’être numérotés par des nombres entiers (1,2,3,…), les places sont numérotées par tous les nombres réels existants entre 0 et 1 (on y retrouve entre autres 0; 1; 0,5; √2/2; π/5; 0,9999999; etc…).
Et pour la première fois depuis son ouverture, le gérant de l’hôtel est nerveux. Après quelques minutes passées à se mordiller la lèvre inférieure, il décide, contrarié, de monter à bord du bus pour annoncer à ses passagers qu’il ne pourra pas tous les accueillir à l’hôtel.
Explication, pourquoi notre gérant n’est-il pas capable d’accueillir ce bus de clients?
Pour montrer que, n’en déplaise à Mlle Bille-en-tête, l’hôtel de Hilbert ne peut pas accueillir ce bus magique, nous allons utiliser un classique des mathématiques : le raisonnement par l’absurde. Nous allons voir que si l’hôtel pouvait accueillir tous les passagers de ce bus, cela nous mènerait à un non-sens.
En effet, imaginons que l’hôtel accueille tous les passagers, nous aurions par exemple:
- Chambre 1: Passager 0,45674329324….
- Chambre 2: Passager 0,13778234432….
- Chambre 3: Passager 0,34254743534….
- Chambre 4: Passager 0,00988328451….
- ….
Prenons maintenant le passager possédant le numéro construit de sorte que sa nième décimale soit toujours égale à la nème décimale du locataire de la chambre n.
Dans notre exemple, son numéro commencerait par 0,4328…
- Chambre 1: Passager 0,45674329324….
- Chambre 2: Passager 0,13778234432….
- Chambre 3: Passager 0,34254743534….
- Chambre 4: Passager 0,00988328451….
- ….
Maintenant prenons chaque décimale de ce nombre et ajoutons lui +1, de sorte que notre numéro se transforme de cette manière sur toutes ses décimales:
0,4329 → 0,5430…
Alors, nous pouvons affirmer que le client correspondant à ce nouveau nombre n’est pas logé à l’hôtel car si il l’était dans une chambre n, sa nième décimale sera différente de celle que nous avons du recenser lorsque nous avons fait le tour des chambres quelques lignes plus haut.
Conclusion, la puissance du continu
Avec l’arrivée du dernier bus, Cantor nous a montré (par l’intermédiaire de l’exemple de Hilbert) que l’infini des nombres réels est ostensiblement plus grand que l’infini des nombres entiers.
Personnellement, cette découverte sur les différences de nature entre infinis continue de me troubler.
Et la question qui doit maintenant vous brûler les lèvres sinon les doigts est: « entre l’infini des réels et l’infini des nombres entiers, il existerait pas un ou des infini(s) intermédiaire(s)? »
Et bien quand, en 1900, au congrès international des mathématiques, David Hilbert présenta sa fameuse liste des 23 problèmes mathématiques irrésolus, la question que vous venez de vous poser était tout en haut de la page: en numéro 1.
Cette question, appelée hypothèse du continu, a finalement été enterrée en 1963 par Paul Cohen (Médaille Fields 1966) qui démontra que le problème était indécidable: c’est à dire que les hypothèses (axiomes) de la théorie des ensembles ne permettaient pas de répondre à cette question. Pour simplifier, l’hypothèse du continu est indécidable au même titre que l‘est la question « devez-vous prendre un parapluie les jours où votre voisin ne porte pas de cravate? ».
[1] Souvent utilisé pour symboliser l’infini, la lemniscate (de Bernouilli) est une courbe plane en forme de huit couché :  … Et oui, sur BlablaSciences on aime aussi apprendre des mots !
… Et oui, sur BlablaSciences on aime aussi apprendre des mots !
[2] L’hétérologisme est la propriété d’une phrase ou d’un mot à ne pas se décrire lui-même (le mot infini n’est pas infini), à l’inverse, s’il correspond à sa définition, il est alors dit autologique (ex: le mot « court » est court).
Cette définition a ça d’amusant qu’elle contient un paradoxe en son sein. En effet, le mot « hétérologique » est hétérologique si et seulement s’il ne l’est pas.
[3] Le principe des tiroirs affirme que si n chaussettes occupent m tiroirs, et si n > m, alors au moins un tiroir doit contenir strictement plus d’une chaussette. Les anglais préfèrent eux parler de pigeons (chacun son truc) et évoque donc le pigeonhole principle.
Références:
Pour la partie philo:
http://www.jbjv.com/La-prudence-de-Descartes-face-a-la.html
http://www.spinozaetnous.org/ftopic-255-20.html
Une vidéo très bien faite sur le sujet:
https://www.youtube.com/watch?v=N_cDA6tF-40