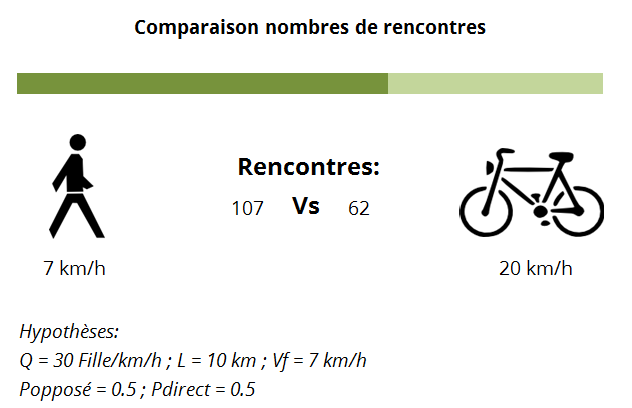
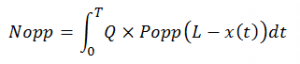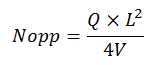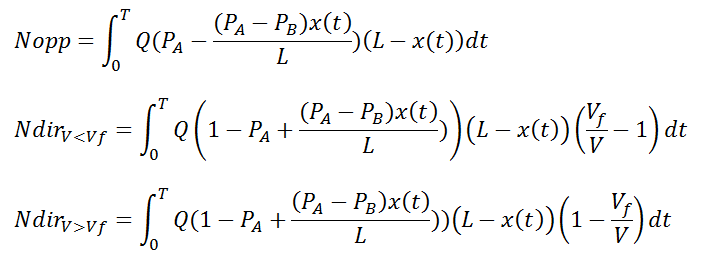Happn vous connaissez? C’est cette application (made in France) qui vous propose de revoir la jolie inconnue croisée au détour d’une ruelle et que vous n’avez pas osé aborder. Et bien aujourd’hui nous allons parler vrai sinon peu: comment maximiser vos chances de rencontre sur un trajet?
Happn ou pas, en réalité le problème est universel: quel moyen de locomotion me permettra de croiser le plus de jolies filles/charmants jeunes hommes lorsque je me déplace d’un point A à un point B.
Introduction – La selle ou les baskets?
Pour simplifier, nous pourrions nous demander quel mode de transport (entre le vélo ou la marche à pied par exemple) permet de croiser un maximum de demoiselles/jeunes hommes.
A priori des arguments prévalent dans les deux camps…
Lorsque je me déplace d’un point A à un point B:
Si je suis à pied, mon temps de trajet sera plus long, j’ai donc plus de chance de croiser des joli(e)s filles/mecs… Toutefois si je suis à vélo, je vais pouvoir dépasser des personnes que je n’aurais pas croisées autrement… En fait, par certains aspects, ce problème se rapproche de cette question que l’on s’est tous déjà posé: « doit-on marcher ou courir sous la pluie? » (Je vous joins à ce titre deux articles aux conclusions opposées: histoire de ne pas trop me mouiller… ohohoh).
[Il faut courir: arguments ici / il faut marcher : arguments ici}
Modèle et calculs théoriques – pour ceux qui veulent comprendre la méthode
Afficher le détail du calculHypothèses:
Pour résoudre ce problème, il nous faut d’abord modéliser un trajet type.
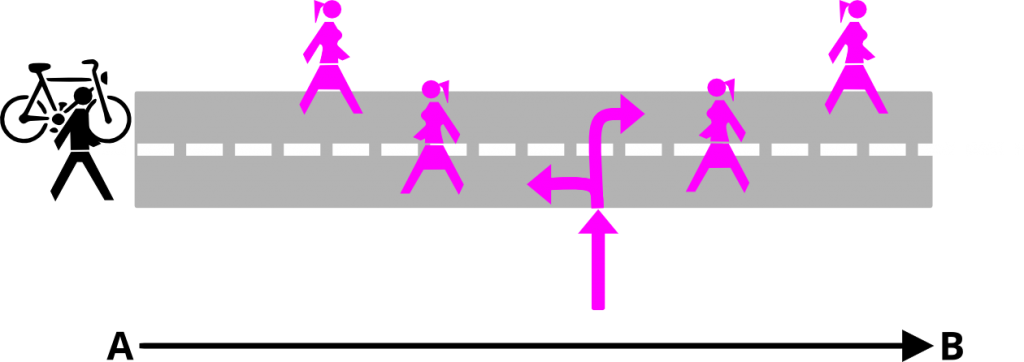
Pour cela, nous allons imaginer une route droite que je m’apprête à parcourir à pied et à vélo entre un point A et un point B.
Je vais donc chercher à comparer le nombre moyen de filles que je croiserai en vélo et à pied en fonction d’un certain nombre de paramètres.
Tout d’abord, je vais donc faire quelques hypothèses:
- Toutes les filles sur la route se déplacent soit dans la direction de mon trajet, soit dans la direction opposée. Finalement, on suppose que les filles qui attendent sur le bord de la route sont en moyenne constante (en nombre…) sur l’ensemble du trajet et on néglige les effets d’heure d’affluence.
- Des filles apparaissent aléatoirement sur le trajet et choisissent de partir à gauche ou à droite.
- Une fois sur le trajet, une fille se déplace jusqu’à atteindre le point A ou le point B (en gros, une fois sur la route elles ne la quittent plus et ne font pas demi-tour).
Une fois ceci établit, nous allons définir:
Q: le nombre moyen de filles par minute et par mètre de trajet qui arrivent sur la route. Popp et Pdir: Les probabilités qu’une fille marche dans une direction respectivement opposée et identique à la mienne. Dans un premier temps nous prendrons Popp=Pdir=1/2.
Vf: la vitesse de marche des filles.
L: la longueur du trajet.
V: ma vitesse.
T: le temps de mon trajet
Enfin, nous distinguerons deux nombres:
Nopp: le nombre de filles croisées qui marchaient dans une direction opposée à la mienne.
Ndir:le nombre de filles croisées qui marchaient dans une direction identique à la mienne.
Calculs:
Il faut d’abord remarquer que Nopp et plus facile à calculer que Ndir pour une raison simple: lorsque que je ne considère que les filles marchant dans une direction opposée à la mienne et que je suis à un point x(t) de mon parcours, toutes (et seulement) les filles qui apparaîtront devant moi (c’est à dire dans un intervalle (L-x(t)) seront des filles que je croiserai. J’obtient alors:
Après intégration, et en prenant Popp=1/2:
Ce résultat est bien sûr valable quelque soit ma vitesse V.
En revanche, lorsque je cherche à calculer le nombre de filles croisées allant dans la même direction que moi, je dois distinguer deux cas:
- Si je marche plus doucement que les filles, certaines me doubleront. Je ne croiserai que les filles qui ont eu le temps de me rattraper avant que j’arrive au point B. C’est-à dire celles me succédant et se situant dans un intervalle que nous nommerons d(t).
- Si je marche plus rapidement que les filles, j’en dépasserai certaines. Je ne croiserai que les filles que j’ai eu le temps de rattraper avant qu’elles n’arrivent au point B. C’est-à dire celles me précédant et se situant dans un intervalle que nous nommerons D(t).
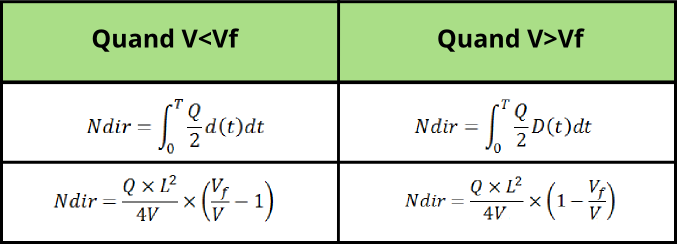
En comparant les temps de trajets restant, on peut définir d(t) et D(t) comme suit :
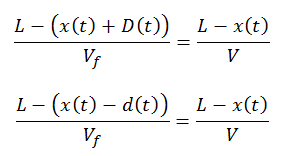
puis calculer les Ndir correspondant à chaque situation (ci-dessous avec Pdir=1/2):
Résultats
Cas standard:
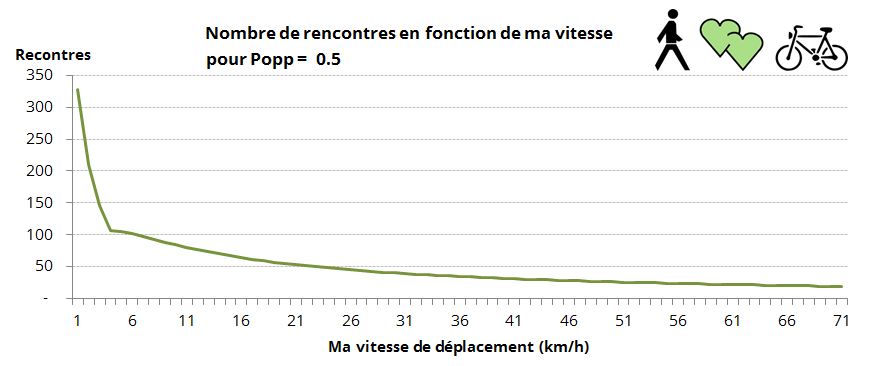
Et bien tout d’abord sachez que si les filles sur mon trajet ont une probabilité égale de se déplacer dans ma direction ou dans une direction opposée à la mienne (Popp=0,5 pour ceux qui ont lu le détail du calcul) alors le résultat est sans appel: la marche à pied est à privilégier.
En fait, il suffit de tracer la courbe représentant le nombre de rencontres faites en fonction de ma vitesse de déplacement sur le trajet, pour se rendre compte que plus on va vite, moins on croise de gens.
Cas d’un trajet vers une zone plus fréquentée:
Toutefois, l’hypothèse consistant à dire que les filles sur mon trajet ont une probabilité égale de se déplacer dans ma direction ou dans l’autre n’est sans doute pas pertinente lorsque je me déplace vers une zone de forte affluence (un concert, un musée, la rue de la soif, …). En effet sur le trajet les gens auront plus tendance à se déplacer vers ce concert/musée/… que dans le sens inverse.
On peut donc s’interroger sur le résultat obtenu lorsque je fais varier la probabilité qu’une fille marche dans une direction opposée à la mienne (Popp).
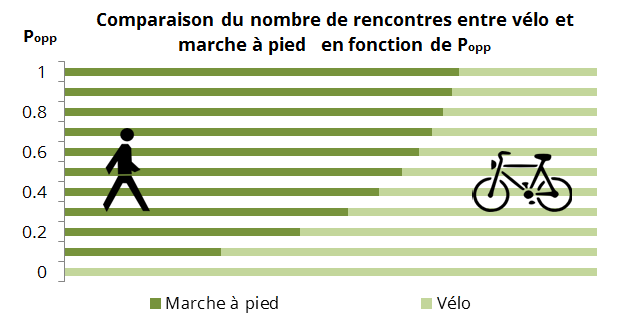
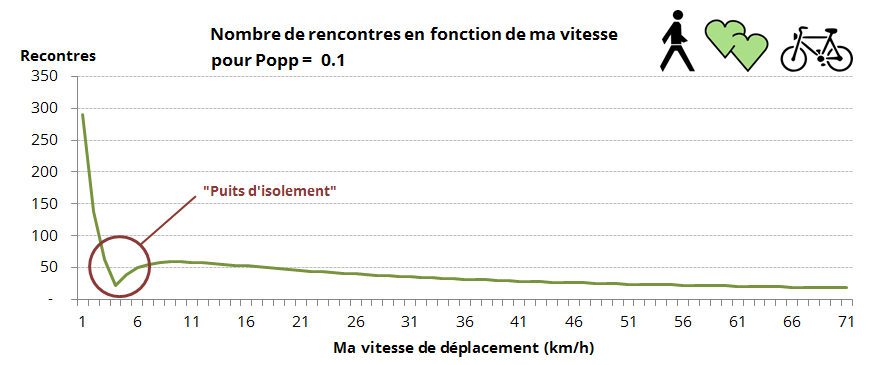
Une fois encore, les chiffres parlent d’eux-même, lorsque sur votre trajet, moins d’une fille sur quatre marche dans un sens contraire au votre: prenez le vélo, vous ferez alors plus de rencontres.
D’ailleurs, chose amusante, pour un Popp<0.5, si l’on trace la courbe représentant le nombre de rencontres faites en fonction de ma vitesse de déplacement sur le trajet, on voit alors apparaître un genre de « puits d’isolement » correspondant à un intervalle de vitesses dans lequel je croiserai significativement moins de monde.
Conclusion: lorsque vous vous déplacez d’une zone peu fréquentée vers une zone très fréquentée : prenez votre vélo. Dans tous les autres cas, préférez la marche à pied et marchez à peine moins vite que d’ordinaire.
Références:
je vous joins mon fichier de calcul Excel [ici].
Pour aller plus loin (à ne lire qu’après avoir lu la partie « Modèle et calculs théoriques »)
Afficher
En fait, les puristes ne seront pas satisfaits avec l’idée d’un Popp constant… et il serait légitime de penser que cette probabilité varie en fonction de x(t).. A priori, si je me déplace vers un concert, plus je me rapprocherai de la zone, plus les gens que je croiserai auront tendance à suivre la même direction que moi.
Allez soyons sport! et regardons ce que donnent les résultats si je modélise Popp par une fonction affine valant Pa au point A et Pb au point B …
Bon la formule est un peu grasse mais le calcul se déroule facilement. Je vous ai mis le résultat et la modélisation en onglet caché dans le fichier Excel joint en ressource. Sans surprise, le résultat est une atténuation du « puits d’isolement » mais on pourrait s’amuser à raffiner encore un peu plus le modèle avec un Popp suivant une loi normale…
Pour ma part, je m’arrête là, il est tard et il est temps pour moi d’aller faire un petit tour expérimental (ou pas).