Qu’il est troublant de voir à quel point notre cerveau est inadapté à l’appréhension des probabilités conditionnelles. Un handicap nous poussant malheureusement parfois à prendre les mauvaise décisions comme l’illustre le paradoxe de Monty Hall.
Une des variantes de ce paradoxe s’appelle le problème des boîtes de Bertrand (du nom du mathématicien français Jean Louis François Bertrand) et en voici une illustration.
Vous faites face à trois boites aux lettres.
– l’une d’elle contient une bonne et une mauvaise nouvelle.
– l’une d’elle contient deux bonnes nouvelles.
– enfin la dernière contient deux mauvaises nouvelles.
On vous propose d’ouvrir une boite aux lettres et vous en sortez une bonne nouvelle.
Avant de piocher la seconde enveloppe, d’après-vous quelle est la probabilité que la deuxième lettre soit aussi une bonne nouvelle?
Solution du problème de Bertrand
Afficher la solution du problème de Bertrand
L’intuition pousse une majorité de personne à répondre 1 chance sur 2. En effet, la première enveloppe vous indique qu’il s’agit soit de la première boite aux lettres, soit de la seconde.
Toutefois, prenons le temps de considérer toutes les issues de tirages possibles avant l’ouverture de la première enveloppe.
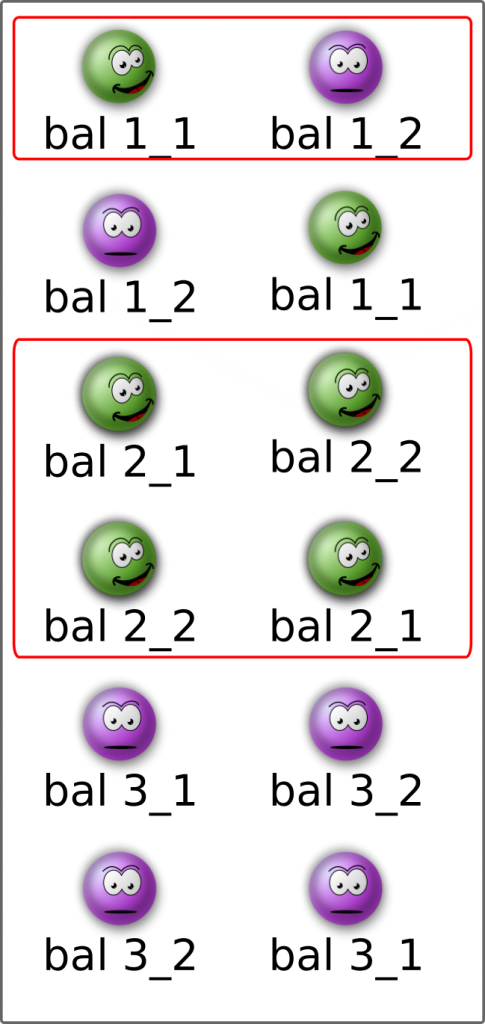(bal=boite aux lettres_numero de l’enveloppe)
Si je me restreint aux issues possibles après le premier tirage, je constate que la probabilité d’obtenir une bonne nouvelle à la deuxième enveloppe est 2/3 et non 1/2…
Illusions cognitives – Extension au problème de Monty Hall
Dans l’expérience de la boite de Bertrand, l’individu oublie souvent que la probabilité de tomber sur une boite aux lettres avec deux nouvelles identiques est plus importante que de tomber sur une boite aux lettres ‘mixte’.
Cette probabilité antérieure au premier tirage est neutre pour le résultat du premier tirage mais possède des répercussions sur les tirages suivants.
Un autre problème utilise ce mécanisme de probabilité masquée pour créer ce que l’on appelle une illusion cognitive.
Imaginez cette fois une rangée de 3 boites au lettres contenant chacune une enveloppe. Parmi ces enveloppes, une seule contient une bonne nouvelle.
Je vous demande de prendre une boite aux lettres, puis, pour maintenir le suspens, je choisi d’ouvrir devant vos yeux une des deux autres boites aux lettres restantes contenant une mauvaise nouvelle.
Il ne reste donc que deux boites aux lettres: celle que vous avez choisie et une autre.
Est-il judicieux à ce moment de changer de boite aux lettres pour espérer tirer la bonne nouvelle?
Solution du problème de Monty Hall
Afficher la solution du problème de Monty HallUne fois encore, une mauvaise intuition nous poussera à dire que les chances d’avoir une enveloppe ou l’autre sont égales. Pourtant, soyez-en sûr, il faut changer de boite aux lettres.
En effet, lorsque vous avez choisi votre boite aux lettres, vous aviez une chance sur 3 de prendre la bonne nouvelle. Si vous décidez de la garder, vous maintenez donc cette probabilité de gain à 1/3.
Lorsque je vous ai volontairement ouvert une enveloppe ‘mauvaise nouvelle’, j’ai possiblement apporté une information.
En fait:
- Soit vous aviez sélectionné une ‘bonne nouvelle’. (1 chance sur 3) Et dans ce cas, j’ai ouvert l’une des deux autres boites aux lettres au hasard (je n’ai pas apporté d’information).
- Soit vous aviez sélectionné une ‘mauvaise nouvelle’. (2 chances sur 3) Et dans ce cas, j’ai choisi d’ouvrir la boite aux lettres contenant l’autre mauvaise nouvelle (et je vous ai apporté une information en vous désignant la ‘bonne’ boite aux lettres à ouvrir).
Il y a donc deux chances sur trois que je vous ai indiqué la bonne boite aux lettres à choisir et il est donc plus judicieux pour vous de modifier votre choix.
Conclusion
Pas toujours facile donc de prendre la bonne décision. Plus tangible que l’allégorie de la caverne, le problème de Bertrand est, à mon sens, une preuve évidente de la difficulté de l’homme à appréhender fidèlement le monde. Alors, au prochain arbitrage, faites vos comptes et ne laissez pas votre intuition vous priver d’une bonne nouvelle.